ডিজিটাল ইলেকট্রনিক্সে লজিক সমীকরণ সমাধান বা সরল করার জন্য বুলিয়ান অ্যালজেব্রায় ডিমর্গ্যান ( Augustus DeMorgan - a nineteenth century English mathematician)-এর দুটি উপপাদ্য ব্যবহার করা হয়। নিচে উপপাদ্য দুটি প্রমাণসহ ব্যাখ্যা করা হলো।
ডি-মরগ্যানের প্রথম উপপাদ্য
দুই বা ততোধিক ইনপুট বিশিষ্ট একটি NAND গেটের আউটপুট ইনপুটে NOT গেট যুক্ত একটি OR গেটের আউটপুটের সমান। অর্থাৎ একটি NAND গেটের ইনপুট A ও B হলে এর আউটপুট,
$\ov{A . B} = \ov A+ \ov B$
ট্রুথ টেবিলের সাহায্যে নিচে ডি-মরগানের প্রথম উপপাদ্য প্রমাণ করা হলো।
| A | B | A.B | $\ov{A.B}$ | $\ov A$ | $\ov B$ | $\ov A + \ov B$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
ডি-মরগ্যানের দ্বিতীয় উপপাদ্য
দুই বা ততোধিক ইনপুট বিশিষ্ট একটি NOR গেটের আউটপুট ইনপুটে NOT গেট যুক্ত একটি AND গেটের আউটপুটের সমান। অর্থাৎ একটি NOR গেটের ইনপুট A ও B হলে এর আউটপুট,
$\ov{A + B} = \ov A.\ov B$
ট্রুথ টেবিলের সাহায্যে নিচে ডি-মরগানের দ্বিতীয় উপপাদ্য প্রমাণ করা হলো।
| A | B | A + B | $\ov{A+B}$ | $\ov A$ | $\ov B$ | $\ov A . \ov B$ |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
চিত্রের মাধ্যমে ডি-মরগ্যানের উপপাদ্য
 |
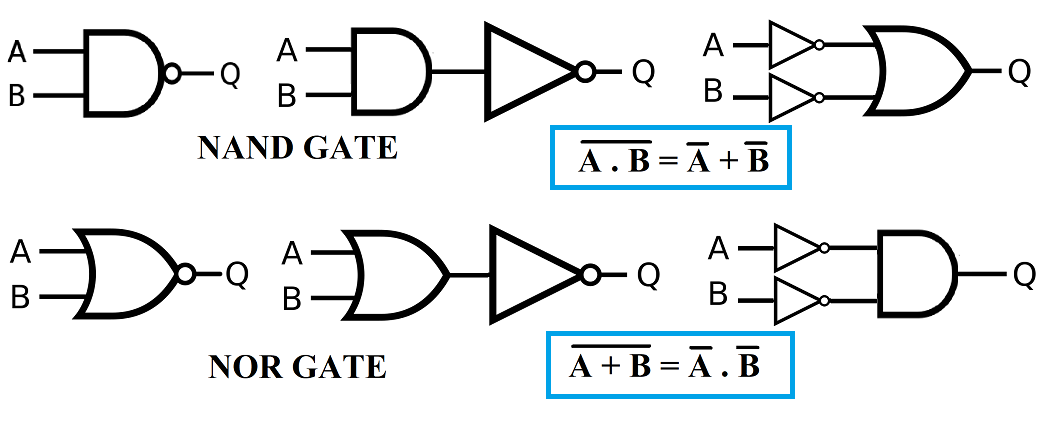| ডিজিটাল ইলেকট্রনিক্সে ডি-মরগানের উপপাদ্য(De Morgan's Law of Digital Electronics) |
কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন