সোর্স ট্রান্সফরমেশন জটিল সার্কিট সরল করার এমন একটি সহজ পদ্ধতি যা বিশেষ করে যেসকল সার্কিটে মিশ্র শক্তির উৎস থাকে সেসকল সার্কিট সরল করার কাজে ব্যবহার হয়। সোর্স ট্রান্সফরমেশন থিওরেমে সার্কিট সরল করতে ভোল্টেজের উৎসকে কারেন্ট উৎসে অথবা কারেন্ট উৎসকে ভোল্টেজ উৎসে রূপান্তরিত করার প্রয়োজন পড়ে।
ভোল্টেজ উৎসকে কারেন্ট উৎসে রূপান্তরের নিয়ম
ভোল্টেজ সোর্সকে কারেন্ট সোর্সে রূপান্তরের জন্য ভোল্টেজ সোর্সের সাথে একটি রেজিস্টর সিরিজ বা সমবায় সমন্বয়ে থাকতে হবে।
ধরি, $V$ ভোল্টেজের সাথে একটি রেজিস্টেন্স, $R$ সিরিজের সংযুক্ত আছে। এক্ষেত্রে ভোল্টেজে সোর্সকে কারেন্ট সোর্সে রূপান্তর করলে কারেন্ট সোর্সের মান, $I = V/R$ হবে, যা নিচের চিত্রে দেখানো হয়েছে।
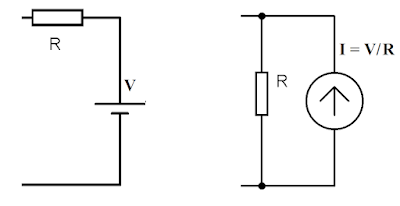 |
| ভোল্টেজ উৎসকে কারেন্ট উৎসে রূপান্তরের নিয়ম |
কারেন্ট উৎসকে ভোল্টেজ উৎসে রূপান্তরের নিয়ম
কারেন্ট সোর্সকে ভোল্টেজ সোর্সে রূপান্তরের জন্য কারেন্ট সোর্সের সাথে একটি রেজিস্টর প্যারালাল বা সমান্তরাল সমন্বয়ে থাকতে হবে।
ধরি, $I$ কারেন্ট সোর্সের সাথে একটি রেজিস্টেন্স, $R$ প্যারালালে সংযুক্ত আছে। এক্ষেত্রে কারেন্ট সোর্সকে ভোল্টেজ সোর্সে রূপান্তর করলে ভোল্টেজ সোর্সের মান, $V = IR$ হবে, যা নিচের চিত্রে দেখানো হয়েছে।
 |
| কারেন্ট উৎসকে ভোল্টেজ উৎসে রূপান্তরের নিয়ম |
একটি উদাহরণের সাহায্যে সোর্স কনভার্শন থিওরেম নিচে ব্যাখ্যা করা হলো।
সমস্যা-১: সোর্স কনভারশন থিওরেম ব্যবহার করে নিচের সার্কিট হতে $R_2$ এর মধ্য দিয়ে প্রবাহিত করেন্ট বের করুন।
 |
| চিত্র-১ঃ সোর্স ট্রান্সফরমেশন |
সমাধান-১
(ক) সার্কিটের দিকে (চিত্র-১) তাকালে আমরা দেখতে পাব যে $5A$ কারেন্ট সোর্সের সমান্তরালে একটি $4Ω$ রোধ রয়েছে। এখন ভোল্টেজ উৎস, $V = IR $ $= 5A ×4Ω = 20V$ এবং একটি $4 Ω$ সিরিজ রোধ এর সাথে প্রতিস্থাপন করি। ভোল্টেজ উৎসের +Ve টার্মিনালটি উপরের দিকে রাখা হয়েছে, কারণ কারেন্ট-উৎস তীরটি উপরের দিক নির্দেশ করছিল।
(খ) আবার সার্কিটের (চিত্র-১) $2V$ ভোল্টেজ সোর্সের সাথে $1 Ω $ রোধ সমান্তরাল আছে। তাই এটিকে কারেন্ট সোর্সে রূপান্তর করেলে, $I = V/R = {2V}/{1 Ω} = 2A$, যা নিচের চিত্রে দেখানো হলো।
(গ) $R_3$ ও $R_4$ সেরিজে থাকায় যোগ করলে নিচের সার্কিট পাওয়া যাবে।
(গ) $20V$-এর ভোল্টেজ সোর্সকে আবার কারেন্ট সোর্সে রূপান্তর করলে নিচের সার্কিট পাব।
(ঘ) এখানে তিনটি রোধ রয়েছে, একটি 1 Ω, একটি 2 Ω ও একটি 7 Ω যার সবগুলি সমান্তরাল। আমরা তিনটিকে একটি সমতুল্য রোধ $(R_{EQ})$ দিয়ে প্রতিস্থাপন করতে পারি, কিন্তু 2 Ω রোধের কারেন্ট বের করতে হবে, তাই আমরা কেবল বাকি দুটিকে একত্রিত করব। এক্ষেত্রে নিচের সার্কিট পাওয়া যাবে।
(ঙ) কারেন্ট সোর্স দুটি প্যারালেল এবং এবং একই দিকে প্রবাহ ঘটাবে। তাই সোর্স দুটোকে যোগ করে $2A + 20\7 A = 34/7A$ পাই।
(চ) উপরের কারেন্ট সোর্সকে আবার ভোল্টেজ সোর্সে রূপান্তর করলে নিচের সার্কিট পাব।
(ছ) সুতরাং $I_2 = 4.25 / {2 + {7/8}} = 1.48A\: (Ans.)$
N.B: অংক করার সময় এতো ব্যাখ্যা করার প্রয়োজন নেই। এখানে বোঝার সুবিধার্থে বিস্তারিত ব্যাখ্যা করা হয়েছে।
ভালো লাগলে অবশ্যই কমেন্টে জানাবেন। আর অন্য কোন বিষয় নিয়ে পরবর্তিতে লিখতে পারি সে বিষয়ে পরামর্শ দিলে আরো ভালো লাগবে। ধন্যবাদ।








কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন