একাধিক সোর্স বিশিষ্ট জটিল সার্কিট সমাধান করা যথেষ্ট সময় সাপেক্ষ এবং কঠিন। জটিল সার্কিট সহজ উপস্থাপন করার একটি জনপ্রিয় পদ্ধতি হচ্ছে থেভেনিন থিওরেম।
থেভেনিন থিওরেম কী
থেভেনিন থিওরেম জটিল লিনিয়ার বাইল্যাটারাল সার্কিট বা নেটওয়ার্ক বিশ্লেষণ করার জন্য এমন একটি পদ্ধতি যা লোড কারেন্ট ও ভোল্টেজ হিসাব করার জন্য উক্ত নেটওয়ার্ককে কেবল একটি ভোল্টেজ সোর্স ও একটি সিরিজ রেজিস্টেন্স দ্বারা প্রতিস্থাপন করে।
থেভেনিন থিওরেম ব্যবহারের নিয়ম
- যে নোডের কারেন্ট বের করতে হবে তা সার্কিট হতে পৃথক করে রাখতে হবে।
- এরপর ওপেন সার্কিট প্রান্তে থেভেনিন ভোল্টেজ, $V_{th}$ এবং থেভেনিন রেজিস্টে, $R_{th}$ বের করতে হবে
- $R_{th}$ বের করার সময় ভোল্টেজ সোর্স গুলোকে শর্ট-সার্কিট এবং কারেন্ট সোর্স গুলোকে ওপেন সার্কিট করতে হবে।
- এরপর $V_{th}$ , $R_{th}$ ও $R_{Load}$ দিয়ে থেভেনিন সমতুল্য সার্কিট আকাতে হবে এবং কারেন্ট বা ভোল্টেজের মান বের করতে হবে।
থেভেনিন্স থিওরেম ব্যবহার করে নিচে কয়েকটি অংক করে দেখানো হলো।
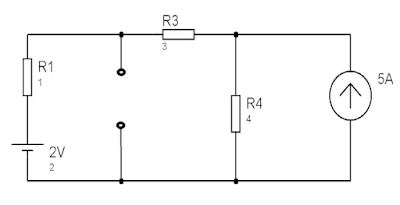
সমস্যা-১: থেভেনিন থিওরেম ব্যবহার করে নিচের চিত্র হতে $I_2$ ও $V_2$ এর মান বের করতে হবে।
সমাধান-১:
-
$R_2$ রেজিস্টর সার্কিট হতে পৃথক করলে নিচের সার্কিট পাওয়া যাবে।
- test$V_{th}$ বের করার জন্য $R_1$ এর মধ্য দিয়ে প্রবাহিত কারেন্ট জানা প্রয়োজন। L1 লুপে KVL প্রয়োগ করে পাই
$2 - I_1R_1 + I_1R_3 + I_3R_4 = 0$
$বা, \, 2 - I_1×1 - I_1×3 - (I_1 + I_2)×4 = 0$ $\[\ \text "P বিন্দুতে KCL প্রয়োগ করে"\ \]$
$বা, \, 2 - I_1 - 3I_1 - (I_1 + 5)×4 = 0$ $\[\ I_2 = 5A\ \]$
$বা, \, 2 - I_1 - 3I_1 - 4I_1 - 20 = 0$
$বা, \, - 8I_1 = 18$
$∴ \, I_1 = -18/8 = -2.25A$
এখন উপরের চিত্র অনুযায়ী KVL প্রয়োগ করে পাই,
$V_{th} = I_1×R_1 + 2 = 2.25×1+2 = 4.25V$
- এখন
থেভিনিন রেজিস্টেন্স, $R_{th} = 1\ || (3 + 4)$ $ = 0.875\ Ω$
- $V_{th}$, $R_{th}$ ও $R_{Load}\, (বা, \, R_2)$ দিয়ে থেভেনিনের সমতুল্য সার্কিট দাঁড়ায়_
$I_2 = {V_{th}}/{R_{th} + R_2} = 4.25/{0.875+2} = 1.48\ A\, (Ans.)$
আগের পোস্টে অন্যান্য থিওরেম ব্যবহারক করে একই সার্কিটের সমাধান করা হয়েছে। নিচে লিঙ্কগুলো দেয়া হলো। চাইলে মিলিয়ে দেখতে পারেন।
কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন